The Three-Body Problem: A Cosmic Dance of Chaos and Order

The three-body problem has captivated mathematicians and physicists for centuries, with its roots tracing back to ancient Greece. This intriguing problem explores the motion of three celestial bodies under their mutual gravitational influence, a deceptively simple yet profoundly complex scenario. While the two-body problem, which deals with the gravitational interaction between two bodies, can be solved analytically, the three-body problem presents a formidable challenge that has stumped some of the greatest minds in history.
The modern formulation of the three-body problem emerged in the late 17th century, primarily due to the groundbreaking work of Sir Isaac Newton. Newton laid the foundation for classical mechanics and universal gravitation in his seminal work, "Philosophiæ Naturalis Principia Mathematica," published in 1687. He successfully solved the two-body problem, demonstrating how two objects, such as the Earth and the Moon, interact under the influence of gravity. However, when it came to three bodies, Newton encountered significant difficulties. He recognized the complexity of the interactions and famously noted that the three-body problem was "a problem of the utmost difficulty."
Despite Newton's insights, the three-body problem remained unsolved for many years. Over the following centuries, numerous mathematicians and physicists attempted to tackle this enigma. Notable figures such as Leonhard Euler, Joseph-Louis Lagrange, and William Rowan Hamilton contributed significantly to understanding celestial mechanics and the dynamics of multiple bodies. Euler and Lagrange, in particular, explored specific cases of the three-body problem, identifying particular solutions and configurations, such as the Lagrange points, where three bodies can maintain a stable position relative to one another. One of the current examples of this can be the James Webb telescope which orbits in one of those Lagrange points.
However, as efforts to solve the three-body problem continued, the system's inherent complexity and chaotic nature became increasingly apparent. The interactions between three bodies can lead to unpredictable and highly sensitive outcomes, where small changes in initial conditions can result in vastly different trajectories. This sensitivity to initial conditions is a hallmark of chaotic systems, making the three-body problem a prime example of chaos theory.
A significant turning point in the study of the three-body problem came in the late 19th century with the work of Henri Poincaré. In 1887, Poincaré published his findings, demonstrating no general analytical solution to the three-body problem. His work revealed that the problem is fundamentally tricky and that the motion of three bodies cannot be expressed in a simple, closed-form solution. Poincaré's insights laid the groundwork for the field of dynamical systems and chaos theory, fundamentally altering our understanding of complex systems in mathematics and physics.
Poincaré's findings also highlighted the limitations of classical mechanics when applied to multi-body systems. The general case remains elusive, while specific solutions exist for certain configurations, such as Lagrange points. This realization has profound implications for celestial mechanics and various fields, including astronomy, astrophysics, and engineering.
The three-body problem continued to inspire research and exploration in the following years. Advances in computational methods and numerical simulations have allowed scientists to study the dynamics of three-body systems in greater detail. By employing powerful computers, researchers can simulate the motion of three celestial bodies over time, providing valuable insights into their interactions and behaviours. These simulations have applications in various fields, including space exploration, where understanding the gravitational interactions between spacecraft and celestial bodies is crucial for mission planning.
Moreover, the three-body problem is relevant beyond classical mechanics. It has implications in molecular dynamics, where the interactions between atoms and molecules can be modelled as a three-body problem. The principles of chaos theory, derived from the study of the three-body problem, have also influenced various scientific disciplines, including biology, economics, and climate science.
In conclusion, the three-body problem is one of mathematics and physics's most challenging and intriguing problems. From its origins in ancient Greece to the groundbreaking work of Newton, Euler, Lagrange, and Poincaré, the quest to understand the dynamics of three celestial bodies has revealed profound insights into the nature of complexity and chaos. While a general analytical solution remains elusive, exploring the three-body problem inspires researchers and deepens our understanding of the universe. As we advance in computational techniques and theoretical frameworks, the mysteries of the three-body problem may yield new revelations, further illuminating the intricate dance of celestial bodies in the cosmos.
Similar Post You May Like
-
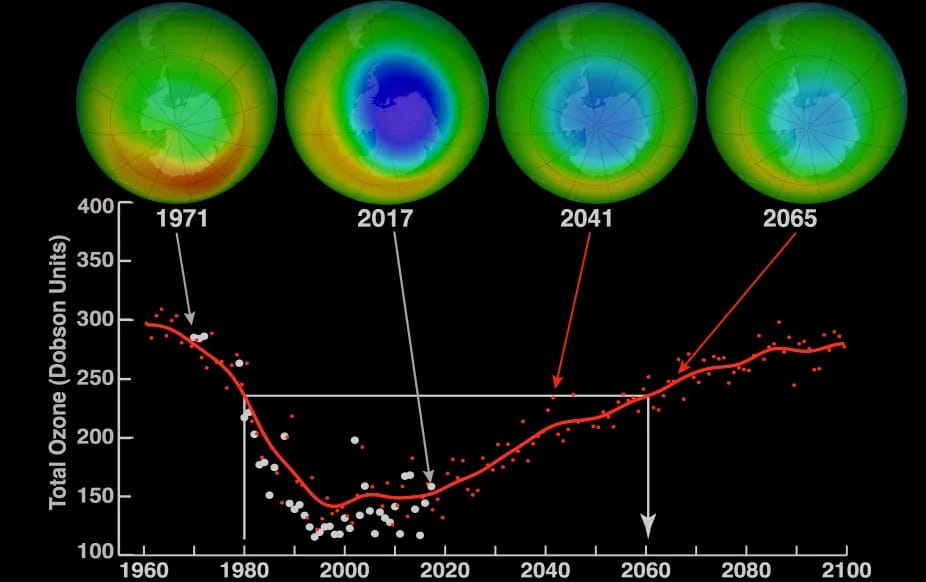
CFCs, HFCs and their long, troubled history
At its peak, the ozone hole covered an area 7 times larger than the size of Europe, around 29.9 million km2, and was rapidly expanding
-

The Origin of Universe: Deciding point where it all began!
Let us unravel and surf through the ideas throughout ages to understand what the universe and its origin itself was to its inhabitants across history.
-

The Artemis Program
Inspired by the Greek goddess of the Moon, twin sister to Apollo, the artimis program was named on 14 May 2019 by Jim Bridenstine.