The Butterfly Effect: Power of Small Changes

Chaos theory, a captivating branch of mathematics, delves into the intricate workings of systems that are highly sensitive to their initial conditions. This phenomenon, often referred to as the "butterfly effect," reveals how seemingly insignificant changes at the outset can cascade into vastly different outcomes, rendering long-term prediction in certain systems virtually impossible. While the name might evoke randomness or disorder, chaos theory actually focuses on complex, deterministic systems whose behavior appears unpredictable due to their extreme sensitivity to starting conditions.
The foundations of chaos theory were laid in the early 20th century, but it gained significant traction in the 1960s through the groundbreaking work of meteorologist Edward Lorenz. While running weather simulations on a rudimentary computer, Lorenz stumbled upon a startling discovery: minute variations in initial conditions could lead to wildly divergent outcomes. This revelation was visually represented in the now-iconic Lorenz attractor, a set of chaotic solutions generated from a simplified model of atmospheric convection.
Several key concepts define the realm of chaos theory:
Sensitivity to Initial Conditions:The defining characteristic of chaotic systems is their extreme sensitivity to the initial state. This is often illustrated by the butterfly effect, which suggests that the fluttering of a butterfly's wings in one part of the world could set off a chain of events that ultimately triggers a tornado in another. In mathematical terms, this means that even infinitesimally small differences in the starting state of a system can lead to drastically different outcomes over time.
Strange Attractors:In a chaotic system, strange attractors offer a visual representation of the system's behavior over time. Unlike regular attractors, which can be points, loops, or other simple geometric shapes, strange attractors possess a fractal structure. This demonstrates that while the system's behavior is unpredictable in detail, it still follows a constrained, non-random path within a specific region of the phase space.
Fractals and Self-Similarity:Fractals are geometric shapes that exhibit self-similarity across different scales. They are often used to describe the complex, repeating patterns observed in chaotic systems. The Mandelbrot set, with its infinite complexity and self-similarity, is one of the most famous examples of a fractal in chaos theory.
Nonlinearity:Chaotic systems are typically nonlinear, meaning that their output is not directly proportional to their input. Nonlinear equations often describe processes where feedback mechanisms lead to exponential growth or decay, making the system's behavior more complex and less predictable.
The applications of chaos theory extend far beyond the realm of pure mathematics, impacting various fields:
Weather Prediction:Chaos theory has profound implications for meteorology. Lorenz's work highlighted the inherent limitations of long-term weather forecasting due to the chaotic nature of the atmosphere. While short-term predictions can be accurate, small uncertainties in initial weather conditions lead to significant errors over time.
Engineering and Robotics:In engineering, chaos theory helps us understand and control complex systems. For instance, in robotics, chaotic algorithms can be used to create more adaptable and resilient machines that can better handle unpredictable environments.
Medicine and Biology:Biological systems, from heart rhythms to population dynamics, often exhibit chaotic behavior. Understanding these patterns can lead to better medical diagnostics and treatments. For example, chaotic models of cardiac arrhythmias help in designing effective interventions for irregular heartbeats.
Economics and Finance:Economic systems can also display chaotic dynamics, where small fluctuations in market conditions can lead to significant economic changes. Chaos theory aids in modeling these systems, helping economists and financial analysts better understand and predict market behavior.
Ecology:In ecology, chaos theory explains fluctuations in animal populations and ecosystems. Predator-prey dynamics, for instance, often follow chaotic patterns, where small changes in population sizes or environmental conditions can result in large, unpredictable changes in ecosystem behavior.
Despite its successes, chaos theory faces several challenges. One major issue is the difficulty in obtaining sufficiently precise measurements of initial conditions to make accurate predictions, especially in complex, real-world systems. Additionally, while chaos theory provides insights into the qualitative behavior of systems, quantitative predictions remain challenging.
Future research in chaos theory aims to refine our understanding of chaotic systems and improve our ability to control and predict them. Advances in computational power and techniques, such as machine learning, offer new avenues for exploring chaotic dynamics and potentially mitigating their unpredictability.
In conclusion, chaos theory revolutionizes our understanding of complex systems by revealing the intricate and often counterintuitive dynamics underlying seemingly random behavior. It emphasizes the limits of predictability in systems that are highly sensitive to initial conditions and has far-reaching applications across various fields, from meteorology to medicine. By studying chaotic systems, scientists and researchers can gain deeper insights into the natural world and develop more effective strategies for managing and predicting complex phenomena.
Similar Post You May Like
-
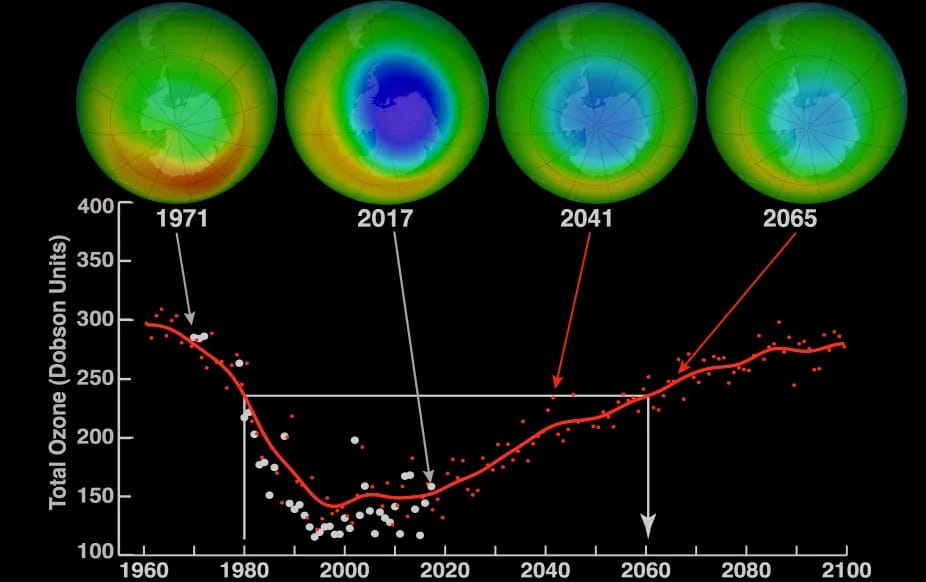
CFCs, HFCs and their long, troubled history
At its peak, the ozone hole covered an area 7 times larger than the size of Europe, around 29.9 million km2, and was rapidly expanding
-

The Origin of Universe: Deciding point where it all began!
Let us unravel and surf through the ideas throughout ages to understand what the universe and its origin itself was to its inhabitants across history.
-

The Artemis Program
Inspired by the Greek goddess of the Moon, twin sister to Apollo, the artimis program was named on 14 May 2019 by Jim Bridenstine.