Unraveling the Mysteries of Infinity: Exploring Zeno's Paradoxes, Infinite Sets, and the Mind-Bending Realm of Large Numbers

Infinity, a concept that transcends our everyday experience of finite quantities, has fascinated philosophers, mathematicians, and thinkers throughout history. From ancient paradoxes that challenge our understanding of motion to the vastness of infinite sets and the mind-bending nature of large numbers, the mysteries of infinity continue to captivate the human mind. In this article, we embark on a journey into the enigmatic realm of infinity, exploring Zeno's paradoxes, different types of infinity, and the awe-inspiring complexities of infinite quantities.
Zeno's Paradoxes: Wrestling with Infinite Divisibility
Zeno of Elea, a Greek philosopher, introduced a series of paradoxes that grapple with the concept of infinity and its implications on motion and change. One of the most famous paradoxes, Achilles and the Tortoise, presents a scenario where Achilles, a swift runner, races against a tortoise. According to Zeno's paradox, Achilles can never overtake the tortoise because each time he reaches the tortoise's previous position, the tortoise has moved slightly ahead, creating an infinite series of distances to traverse.
These paradoxes highlight the paradoxical nature of infinity and the challenges it poses to our intuitive understanding of continuous motion and change. While these paradoxes have sparked debates and discussions for centuries, they also serve as thought-provoking puzzles that invite exploration into the nature of infinity and its philosophical implications.
Different Types of Infinity: Countable vs. Uncountable Sets
In mathematics, infinity is not a singular concept but rather a diverse landscape with different types of infinities. One fundamental distinction is between countable and uncountable sets, as elucidated by Georg Cantor, the pioneer of set theory.
Countable sets, such as the set of natural numbers (1, 2, 3, ...) or integers, have an infinite but enumerable number of elements. Each element in a countable set can be assigned a unique position or "counted" in a systematic manner, even though the set itself is infinite.
Uncountable sets, on the other hand, possess a higher level of infinity and cannot be put into one-to-one correspondence with the natural numbers. The set of real numbers, including all rational and irrational numbers, is an example of an uncountable set, demonstrating the vastness and complexity of infinite quantities beyond our intuitive grasp.
Mind-Bending Nature of Large Numbers: Beyond Human Comprehension
As we venture into the realm of large numbers, the mind encounters challenges in conceptualizing quantities that exceed our everyday experience. The scale of large numbers, whether in the context of astronomical distances, particle physics, or combinatorial mathematics, stretches the limits of human comprehension.
For instance, consider the number of atoms in the observable universe, estimated to be around 1080. This astronomical figure, known as a googol, represents a quantity so vast that it surpasses our ability to visualize or grasp its magnitude intuitively.
Moreover, concepts such as Graham's number, a gargantuan number used in mathematical proofs, or Skewes' number, a theoretical limit in number theory, demonstrate the mind-bending nature of large numbers and their role in pushing the boundaries of mathematical exploration and understanding.
Conclusion: Navigating the Infinite
In conclusion, the mysteries of infinity encompass a rich tapestry of philosophical conundrums, mathematical complexities, and cognitive challenges. From Zeno's paradoxes that question the nature of motion to the exploration of different types of infinity and the awe-inspiring scale of large numbers, infinity permeates multiple domains of human inquiry.
While infinity may elude full comprehension, its exploration fuels intellectual curiosity, inspires mathematical innovation, and invites contemplation of the profound mysteries that lie beyond the finite realm. As we grapple with infinity's enigmatic nature, we embark on a perpetual journey of discovery, where each question leads to new insights and the infinite possibilities of human thought.
Similar Post You May Like
-
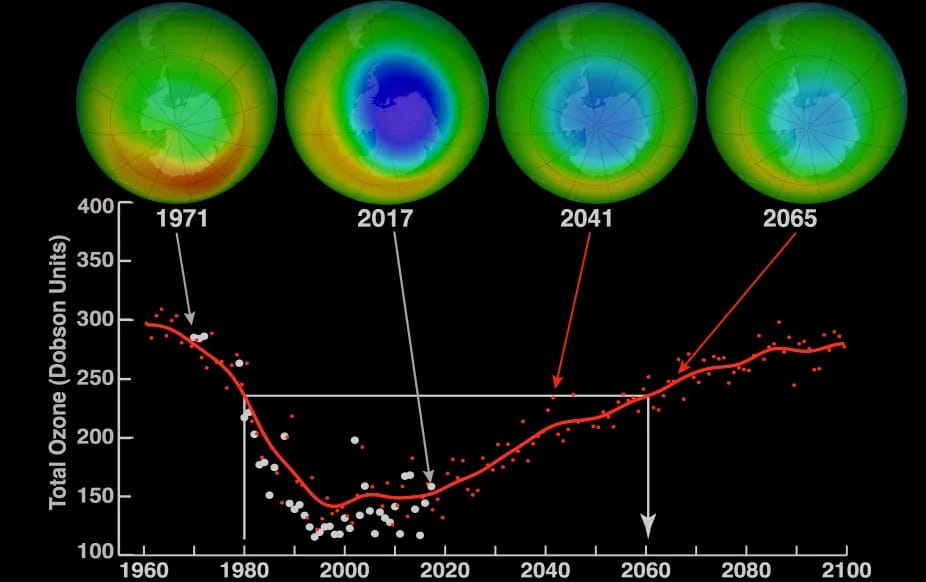
CFCs, HFCs and their long, troubled history
At its peak, the ozone hole covered an area 7 times larger than the size of Europe, around 29.9 million km2, and was rapidly expanding
-

The Origin of Universe: Deciding point where it all began!
Let us unravel and surf through the ideas throughout ages to understand what the universe and its origin itself was to its inhabitants across history.
-

The Artemis Program
Inspired by the Greek goddess of the Moon, twin sister to Apollo, the artimis program was named on 14 May 2019 by Jim Bridenstine.